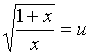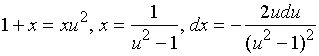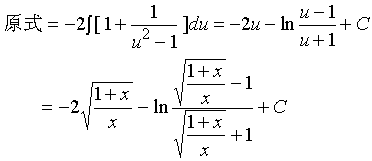§4.4 特殊类型函数的积分举例

一、有理函数积分

1、有理函数与有理函数的积分

有理函数是指两个既约多项式之商所表示的函数，它具有如下形式：

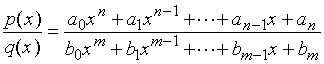
其中：和均为正整数或零； 及均是实数，且、，多项式与之间无公因子。

若， 称它为真分式；

若， 称它为假分式。

形如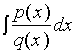的不定积分称为有理函数的积分。

若是假分式，利用多项式的除法， 总可以将假分式化成多项式与真分式之和的形式。例如：

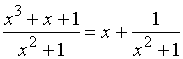
多项式的积分我们已经会求，因此，计算的关键是：

当为真分式时，如何求。

2、代数学中的一个结论

设为真分式， 若多项式在实数范围内能分解成一次因子和二次质因子的乘积，即：

其中： 是正整数。

则 可以分解成下列 部分分式之和

常数 可利用待定系数法来确定。

【例1】求

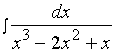
解：被积函数分解成部分分式

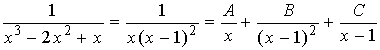
通分得

令 得

令 得

令 得 ， 有

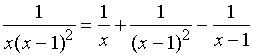
于是， 有

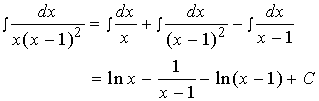
【例2】求

解：

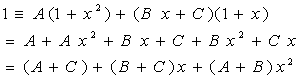
比较恒等式两端有：

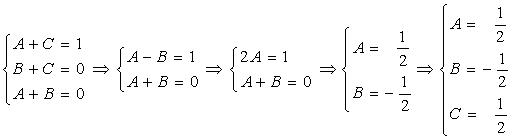
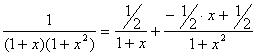
二、三角函数有理式的积分

1、何谓三角函数的有理式

三角有理式是指由三角函数和常数经过有限次四则运算所构成的函数。

由于三角函数都可用及的有理式表示， 故三角有理式也就是与的有理式。记作，其中表示两个变量与 的有理式。

2、万能替换

三角有理式的积分 均可通过替换将它转化成关于的有理分式函数的积分。

事实上， 有

，

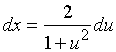
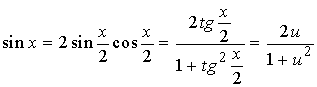
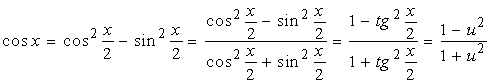
那么，三角有理式的积分为

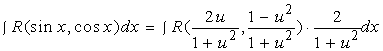
由于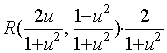是的有理分式函数，而有理分式函数的积分可以化为部分分式的积分，因此，可以说三角函数有理式的积分问题也获得了完满的解决。

【例3】求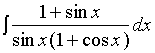

解：令

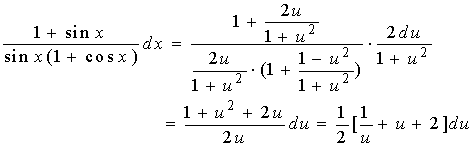
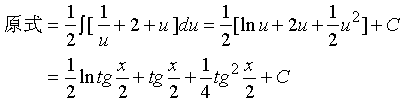
【例4】求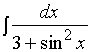

解：令

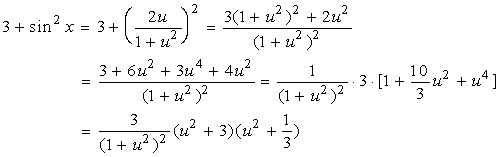
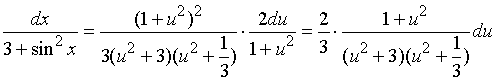
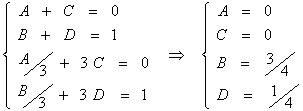
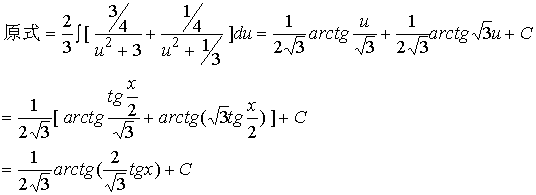
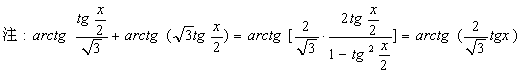
【例4解法一】

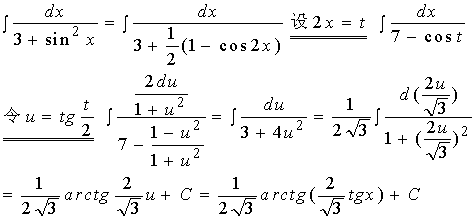
【例4解法二】

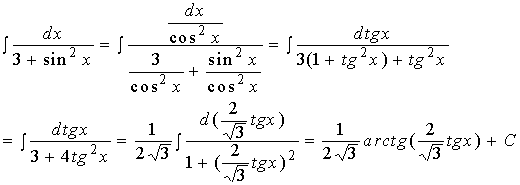
三、简单无理函数的积分

一般说来，无理函数的积分十分地复杂，有些无理函数甚至无法求出用有限形式表示的原函数。

这里， 我们仅讨论 及 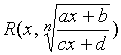这两类简单无理函数的积分， 其中是、这两个变量的有理式。

【例5】求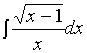

解：令 ， ，

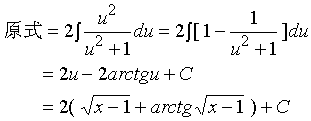
【例6】求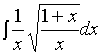

解：令